Stephen Hara

Hi there! Today, I was writing a different blog post, but it started getting pretty long, so I decided to pivot and talk about something a little simpler: Monte Carlo simulations!

I first learned about the Monte Carlo method of calculating answers to probabilistic situations in university as part of a class on numerical methods. To quickly summarize: given some scenario with non-trivial but easily understood base probabilities, rather than going through the complicated process of determining the concrete answer of any particular question, in a Monte Carlo simulation you instead make a large number of observations based on the known probabilities to answer the question.

In that class, we used it to estimate integrals for a function over a specified range. Building up to that can be done in a few high-level steps:

1. First, we need to be able to calculate the function;
2. Then, we need to take randomized samples within the range;
3. Last, we need to accumulate a large number of samples and average them, then multiply that by the range

The average of all those samples will be the integral over the range. Let's build a Monte Carlo simulation for the square function: $f(x) = x^2$

First, let's make our function.

function square(x) {
  return x * x;
}

Simple enough! Let's also try to call it a number of times:

for (var i = 0; i <= 10; i++) {
  console.log(i, square(i));
}

// results in...
0 0
1 1
2 4
3 9
4 16
5 25
6 36
7 49
8 64
9 81
10 100

Cool! Next, how can we take randomized samples? We'll need to use the Math.random() function in JS to get a random number between 0 and 1. Since we'll likely want to use a different range - say, -10 to 10 - we have to do a little bit of finagling and math.

We can use the random number as a measure of how far into the range we want to sample. Then, we multiply the random number by the total range, and add the lower limit of our range to that result, and that will give us the value for "x" we sample.

for (var i = 0; i <= 10; i++) {
  const lowerLimit = -10;
  const upperLimit = 10;
  const range = (upperLimit - lowerLimit);
  const sample = lowerLimit + (Math.random() * range);
  console.log(sample, square(sample));
}

// example output
0.2442285408573639 0.059647580169317066
3.845802381476089 14.790195957367157
-0.5799238892346903 0.33631171730508935
8.47264325104629 71.78568365950024
8.705075937763862 75.77834708223538
-1.4103879134353559 1.9891940663645369
-5.962861318180601 35.555715099854496
-7.21220376021984 52.01588307892919
-5.478958693659344 30.0189883668253
-7.5575637333194035 57.11676958318472
2.1570867021239906 4.653023040480154

Great! We're almost there. Now we just need to add up all the samples, average, and multiply:

// set some of our future values up here
var sum = 0;
const sampleCount = 100000;
const lowerLimit = -10;
const upperLimit = 10;
const range = (upperLimit - lowerLimit);

for (var i = 0; i <= sampleCount; i++) {
  // get the sample location...
  const sample = lowerLimit + (Math.random() * range);
  // and add the sample result to the rolling sum
  sum += square(sample);
}

// make a rectangle (as described below)
const result = range * (sum/sampleCount);

// technically 2000/3 but #fractionsincode
const expectedAnswer = 666.6666667;
// find out how wrong the estimate is
const error = Math.abs(expectedAnswer - result);
const errorPercent = error/expectedAnswer * 100;

// some pretty output
console.log(`Approximate area under the curve for range [${lowerLimit}, ${upperLimit}]: ${result}`)
console.log(`Error of ${error} (${errorPercent}%)`)

// here's a couple of runs
Approximate area under the curve for range [-10, 10]: 667.6623214481579
Error of 0.9956547481579037 (0.14934821221621816%)

Approximate area under the curve for range [-10, 10]: 666.6071783517447
Error of 0.05948834825528593 (0.008923252237846726%)

Approximate area under the curve for range [-10, 10]: 663.6055831735898
Error of 3.0610835264101297 (0.45916252893856135%)

And that's pretty much it! As you can see, it's not perfect, but it's not too wrong if you just need to get an estimate. Plus, it's pretty simple!

Summary

Monte Carlo simulation is a great way to explore problem spaces. I've previously used it to simulate leveling gathering jobs in Final Fantasy 14 as I talked about in a blog post a couple years ago. Unfortunately the code is missing and I'm not sure where it is, but once I find it I'll update that post!

If you enjoyed this post, why not subscribe to my newsletter?

Appendix: Why Multiply By the Range?

I sorta forgot that you need to multiply by the range when I started working on this post, and it wasn't quite clear to me why the initial answers were wrong, so I figure it might be helpful to re-hash my re-learning. For posterity!

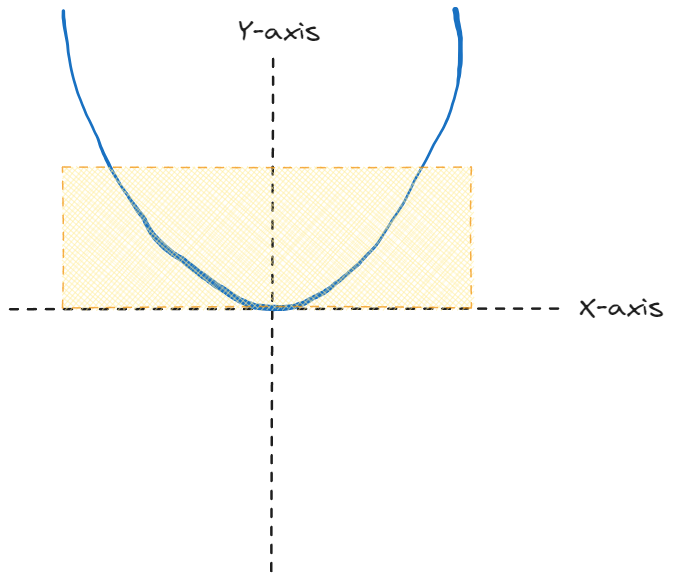
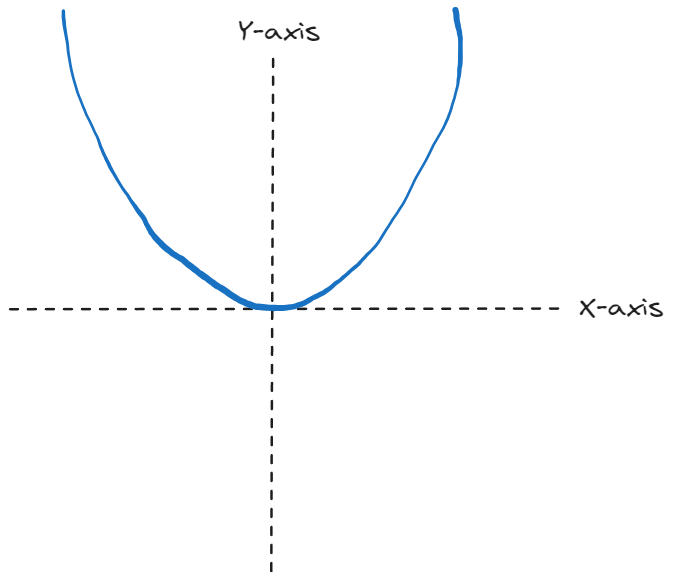
Let's start with a very crude sketch of our function, $x^2$:

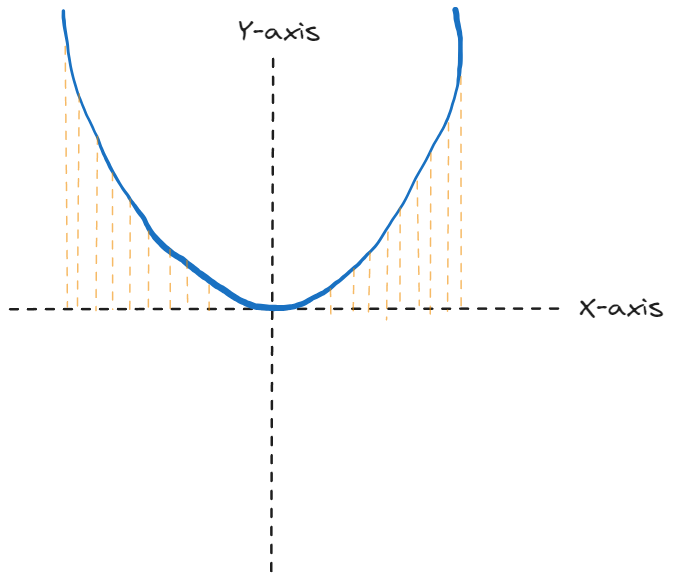
When we do the sampling process, we end up getting the height of the function at a bunch of random spots on the x-axis:

When we then divide by the number of samples, we get the estimated average height of the function across the range. In order to get the estimated area, we need to turn it into a rectangle, so we multiply it by the range - or, the length of the desired rectangle.